05-16-2017, 06:34 AM
Heron-İç teğet çember arasındaki güzel bir ilişki
Alıntı:
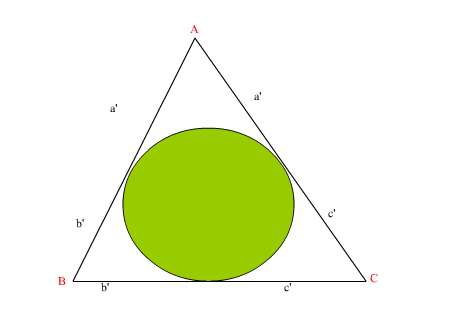
Teorem.Bir üçgende yukarıdaki gibi a',b',c' yarıçaplı çemberler çizilirse,
Alan=√a'b'c'(a'+b'+c')
bağıntısı elde edilir.
İspat.
Elimizde ne bir açı ne bir diklik var.İkisi de yok.Bakacak halimizde yok! Akıllarıza hemen heron formülü gelmeli , gelmediyse gelmiş oldu!
a',b',c' değerlerini bilmemiz demek bizim üçgenin üç kenarını da bilmemiz demektir.
Şimdi şuna bir göz atın-aslında açıortayın bölme oranı şeklinde bir konu açıp bunu da kanıtlayacağım ama işlem gereği kanıtlamaya gerek kalmadan şunu çıkarabiliriz;
u-a=(a'+b'+c')-(b'+c')=a'
u-b=(a'+b'+c')-(c'+a')=b'
u-c=(a'+b'+c')-(a'+b')=c'
Sarılacivertli ifadeler apaçık heron formülünü işaret ediyor.
Derhal yerine yazalım.
|ABC|=√u.(u-a)(u-b)(u-c) şeklinde yerine yazarsak ispatımızı tamamlamış oluruz.
Şimdiyse bu teoremle ilgili bir örnek çözelim.Olsun bitsin!